How to Calculate Steel Weight Per Foot (+ Formulas & Calculator)

Want to know how heavy a foot of steel is? Find the shape’s end area, multiply by 1 foot (for volume), then multiply by how heavy steel is for its size (its density – around 490 lbs/ft³).

Key Takeaways (Quick Guide)

• Simple Math: Weight = Space it takes up × How heavy steel is. For ‘per foot’, use the end area × 1 foot length.
• Steel’s Heft: Steel’s density is key. It’s about 490 pounds for a cubic foot block (or 0.283 lbs per cubic inch / 7850 kg per cubic meter).
• Shape is Everything: Round bar? Flat plate? Angle? Need the right math for that end area.
• Watch Your Units!: Inches with inch density, feet with foot density. Keep ’em matched!
• Calculators Help: Our steel weight calculator below does the math for you — just plug in the numbers.

How to Use This Calculator

Makes it easy! Just:

1. Pick the Shape: Tell it if you have a round bar, square, flat, angle, or pipe.
2. Type in Sizes: Put in the measurements it asks for (like width, thickness, diameter). Use inches or mm as it says.
3. Tell it the Length: How long is the piece? If you just want the weight per foot, put ‘1’ in the foot box (or 12 inches, etc.).
4. Hit Calculate!
5. See the Weight: It’ll pop up the estimated weight, usually in pounds (lbs) and kilograms (kg).

Heads up: This uses a common steel density number. Real-world steel might weigh just a tiny bit different.

The Basic Idea Behind Steel Weight

So how does this work anyway? It’s pretty simple, really. Everything has weight based on how much space it fills and how “packed” that material is.

Weight = How much space it takes (Volume) × How packed the stuff is (Density)

Steel is packed. It’s dense stuff. A small piece weighs a lot more than the same-sized piece of wood or plastic.

Now, if we want the weight for just one foot of steel length, we need the volume of that one-foot piece. Imagine slicing the steel bar or pipe – the area of that cut end is the cross-sectional area.

Volume of One Foot = Area of the Cut End × 1 Foot Length

So, find that end area, multiply by 1 foot (making sure units match!), then multiply by steel’s density. Boom, weight per foot.

Steel’s Density Number (The Important Bit)

Different steel types vary slightly, but for most calculations with regular carbon steel, you can use these numbers:

• Pounds: About 490 lbs per cubic foot (lbs/ft³)
  • Or, if using inches: About 0.283 lbs per cubic inch (lbs/in³)
• Kilograms: About 7850 kg per cubic meter ( kg/m³)
  • Or, if using cm: About 7.85 g per cubic centimeter (g/cm³)

Super Important: If you measure your steel in inches, use the density number for cubic inches (0.283 lbs/in³)! If you measure in feet, use the cubic foot number (490 lbs/ft³). Mixing them up gives crazy, wrong answers.

Figuring Out the End Area for Common Shapes

This is where the shape matters. Here’s how to get that cross-sectional area (make sure you measure everything in the same units, like inches):

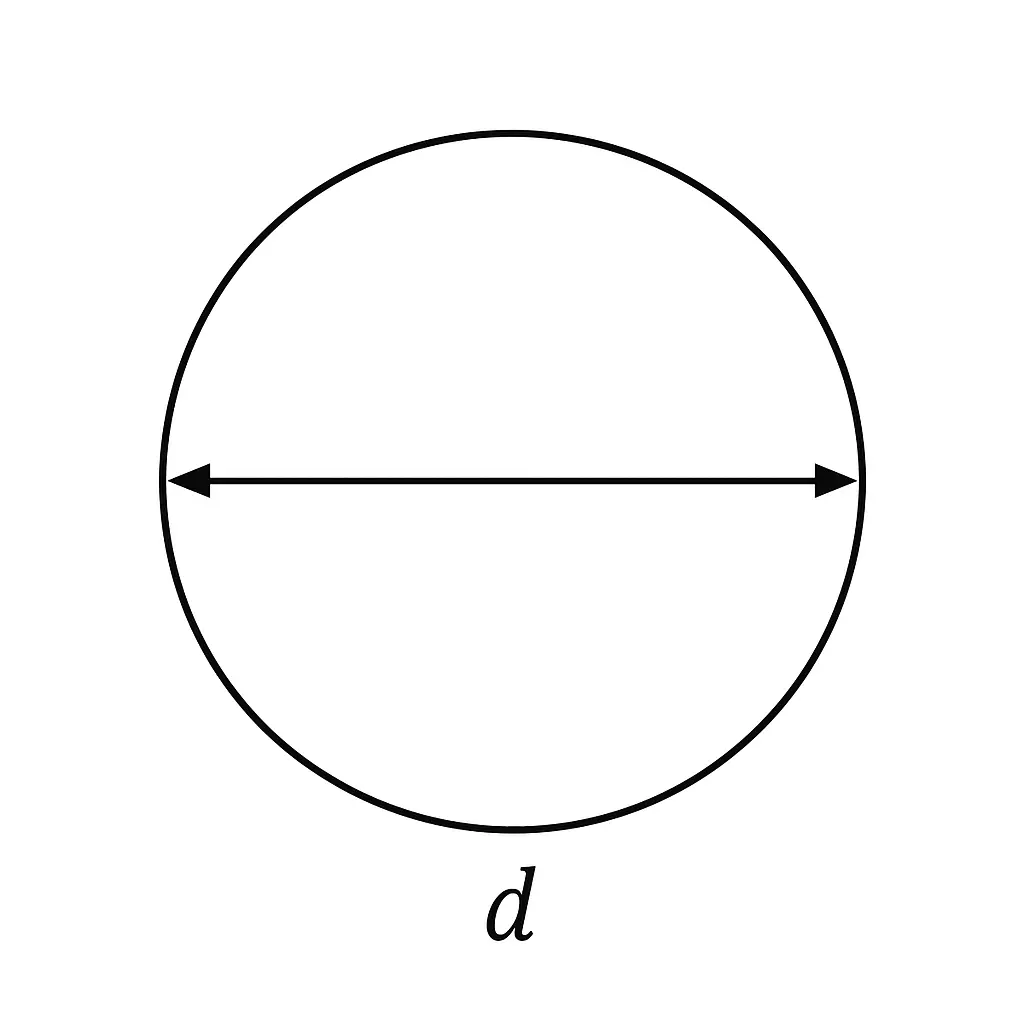
1. Round Bar

• Need: Diameter (d) – the distance across the circle.
• Area Math: Area = 3.14159 × (Diameter ÷ 2) × (Diameter ÷ 2)
  • (That’s Pi times the radius squared)
• Weight per Foot (Example using inches): Find Area in square inches, then do: Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

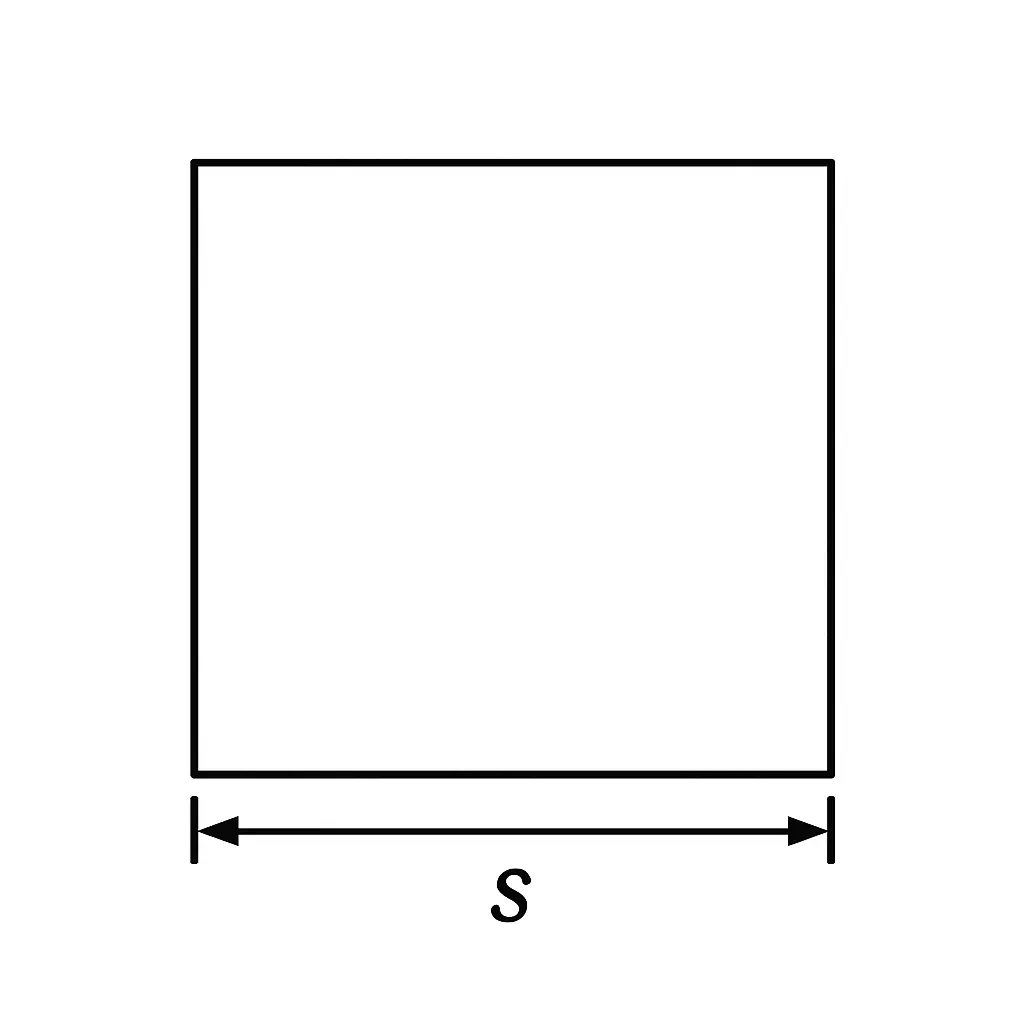
2. Square Bar

• Need: Length of one side (s).
• Area Math: Area = Side × Side
• Weight per Foot (Example using inches): Find Area in square inches, then do: Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

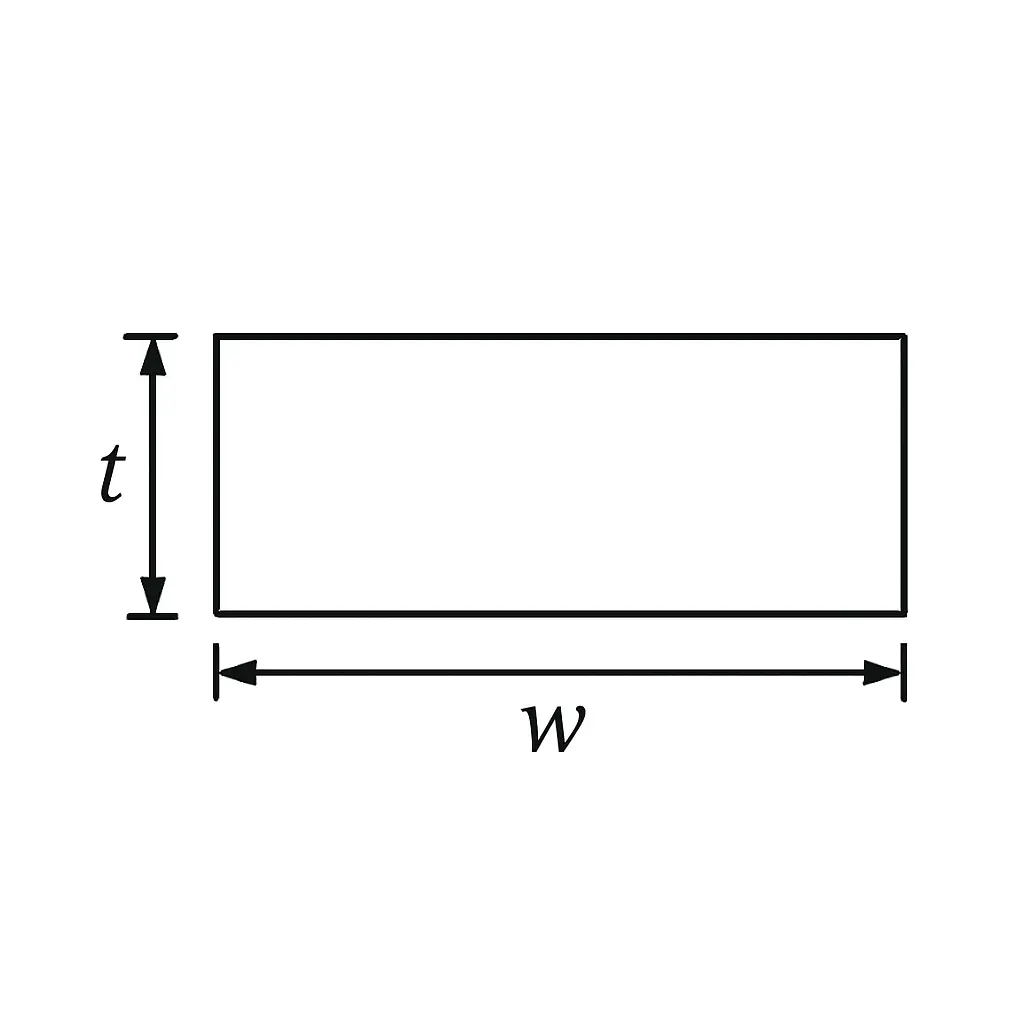
3. Rectangular Bar / Flat Bar / Plate

• Need: Width (w) and Thickness (t).
• Area Math: Area = Width × Thickness
• Weight per Foot (Example using inches): Find Area in square inches, then do: Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

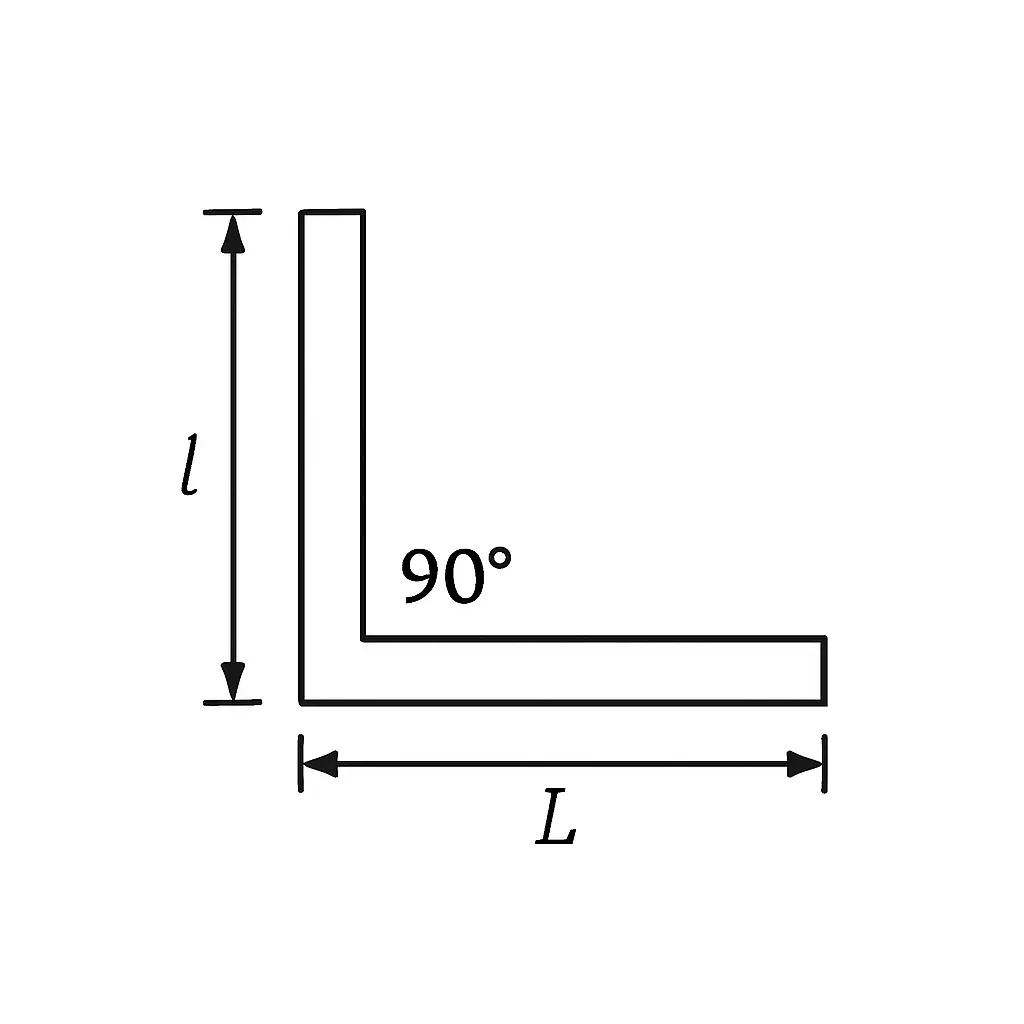
4. Angle Iron (L-Shape, Equal Legs for simplicity)

• Need: Length of one leg (L) and how thick the metal is (t).
• Area Math (Close Enough): Area ≈ (2 × Leg Length × Thickness) – (Thickness × Thickness)
  • Think of it as two rectangles minus the corner square where they overlap.
• Weight per Foot (Example using inches): Find Area in square inches, then do: Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

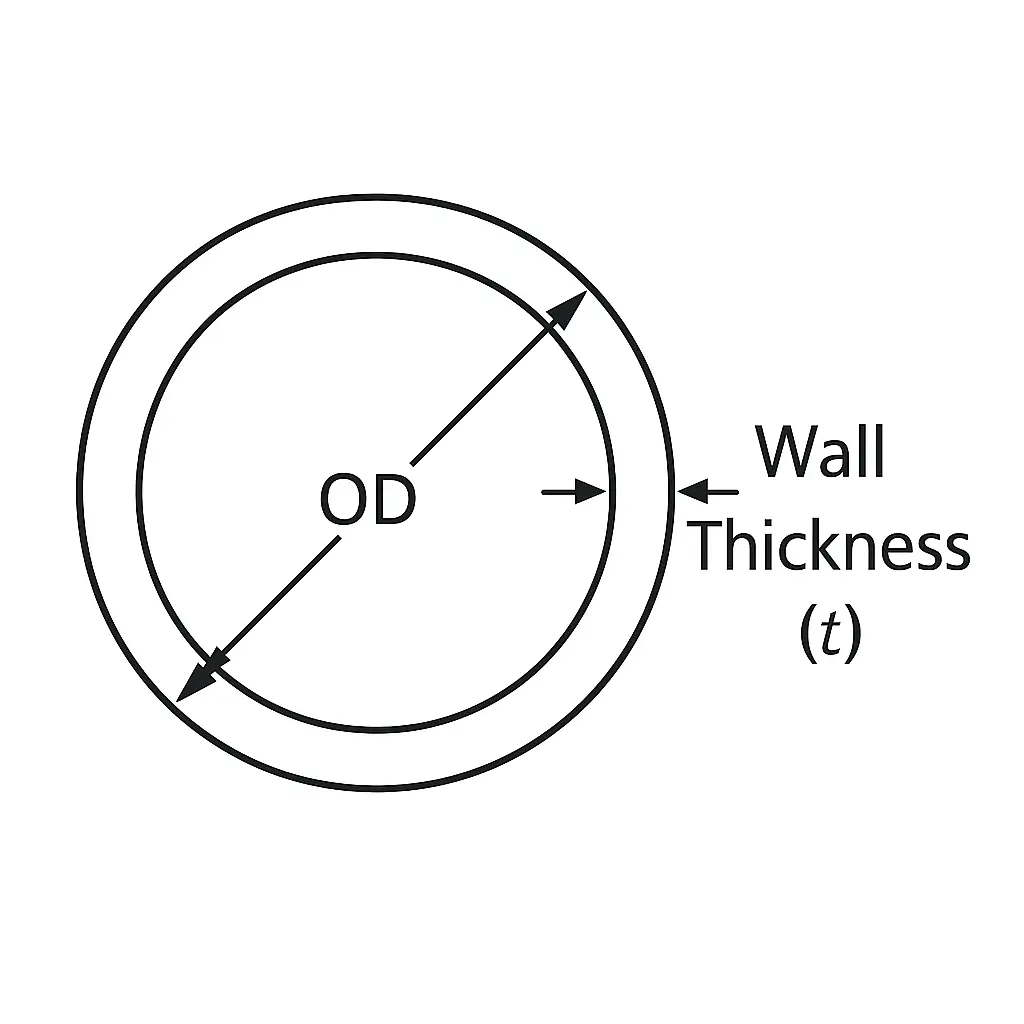
5. Steel Pipe / Round Tube (Hollow Circle)

• Need: Outside Diameter (OD) and how thick the wall is (t).
• Area Math: Find the area of the whole outer circle, then subtract the area of the inner hole.
  • Outer Circle Area = 3.14159 × (OD ÷ 2) × (OD ÷ 2)
  • Inner Diameter (ID) = OD – (2 × t)
  • Inner Hole Area = 3.14159 × (ID ÷ 2) × (ID ÷ 2)
  • Metal Area = Outer Circle Area – Inner Hole Area
• Weight per Foot (Example using inches): Find Metal Area in square inches, then do: Metal Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

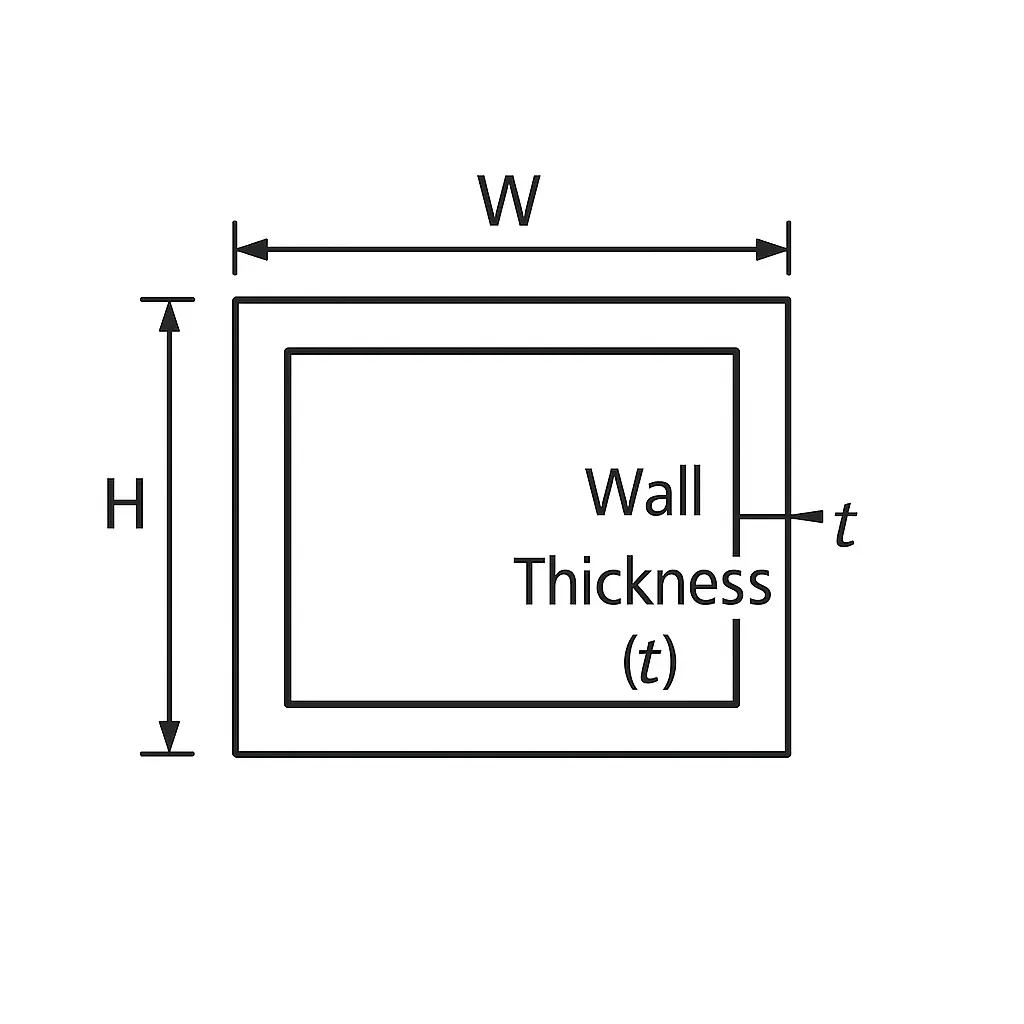
6. Square or Rectangular Tube (Hollow Box)

• Need: Outside Width (W), Outside Height (H), Wall Thickness (t).
• Area Math (Close Enough): Area ≈ [2 × Width × Thickness] + [2 × (Height – 2 × Thickness) × Thickness]
  • Basically adding up the areas of the four skinny rectangles that make the walls.
• Weight per Foot (Example using inches): Find Area in square inches, then do: Area × 12 inches × 0.283 lbs/in³ = Weight in lbs.

Quick Note: These formulas work, but getting them perfect for tricky shapes can be complex. That’s why calculators are handy – they handle the exact math.

Why Figure This Weight Out Anyway?

Knowing weight per foot helps a lot:

• Costing Jobs: Steel often sells by weight. Know the weight, know the cost (roughly).
• Shipping Stuff: Need to know the total weight for shipping quotes and how to lift it.
• Building Plans: Engineers need weights for designs.
• Keeping Track: Easier to manage your steel stock if you know weights.
• Checking Orders: Did you get what you paid for? A weight check helps verify.

That’s Pretty Much It!

So yeah, finding steel weight per foot is just about finding the end area, multiplying by length (like 1 foot), and multiplying by how dense steel is. Shape matters for the area calculation. Keep your units straight (inches with inches, feet with feet). Or just use a calculator online – makes life easier!